对于行测考试中的图形推理题型，有些同学可能已经采取了“放弃治疗”的态度，具体表现就是在做题时盯着题目看，到底选哪个呢?随缘吧!于是随便勾一个。至于对不对?看命吧!但是其实有很多图形推理的题目考查的都是一些常见的规律，而我们需要做的就是熟练掌握这些常见规律并结合题目特点进行运用。在这些常见规律中，有一个规律在考试中出现的频率高，但是大家又很容易遗忘，那就是一笔画&多笔画的问题，也就是看一幅图能否不重复、不间断地一笔描出来，如果能，那就是一笔画图形;如果不能，那就是多笔画图形。但是拿到一幅图的时候我们如何去判断它是不是一笔画图形呢?有些同学可能认为，直接画一画就行了，能画出来就是，画不出来就不是。但这样解题会遇到两个问题：第一是占用的时间较多;第二是如果画不出来的话又会陷入纠结“到底是它本来就不是一笔画图形，还是其实它是一笔画但我自己没有找到一笔画出来的方法呢?”为了解决这些问题，我们引入了一个新的概念，叫做“奇点”，从而把线的问题转化为点的问题，然后直接“计算”出笔画数，判断起来更快、更准确。那么今天就带大家一起来学习一下这种方法!

 

　　一、方法透析

 

　　1. 奇点的含义：如果从一个点出发的线条数为奇数，我们就称这个点为“奇点”。

 

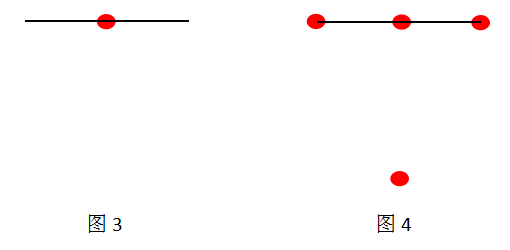
　　这里需要理解：“出发”不等于“经过”，“出发”是指每次都以该点为出发点开始数，如图1所示，从标红点出发的线条有5条，5是奇数，所以该红点是奇点;“线条数”包括直线数和曲线数，如图2所示，从标红点出发的线条有3条，3是奇数，所以该红点是奇点。

 

　　2. 判断笔画数

 

　　我们需要做的是判断图形中的所有点是不是奇点，最后根据奇点的个数判断笔画数，判断方式如下：

 

　　一笔画图形：奇点数为0或2

 

　　多笔画图形：最少笔画数=奇点数÷2

 

　　二、注意事项

 

　　掌握了基本的方法之后同学们可以自己尝试判断下列图4是几笔画图形。

 

　　

 

　　同学们看到图4的时候可能第一反应就是整幅图总共就1个交点，那当然只有一个奇点了。但是这个结果是错误的，忽略了端点。其实，端点也是奇点，因为从端点出发的线条只有1条，而1是奇数，所以端点也是奇点。因此上图应该有4个奇点，如图5所示，为2笔画图形。

 

　　所以，大家在做题的时候一定要注意不要遗漏了端点。事实上，平面图形中的奇点个数一定是偶数，如果大家数出来的个数是奇数，那意味着数错了，需要重新数。

 

　　三、适用范围

 

　　大家可以用前面的方法来判断一幅简单的图形，如图5所示：

 

　　

　　有些反应比较快的同学可能会迅速判断：奇点数为0，一笔画图形。但是只要大家还尚存一丝“理智”，就会发现我们画完正方形之后在不间断的情况下画出里面的圆形。那这是不是以为着我们的方法存在问题呢?其实不是，只是我们的方法有一定的适用范围：

 

　　适用范围：只有一个部分的图形

 

　　多部分图形的笔画数=各部分笔画数之和

 

　　观察图5，发现正方形和圆形完全没有公共点，是两个不同的部分，判断笔画数是需分开来看。正方形的部分没有奇点，是一笔画图形;圆形的部分也没有奇点，是一笔画图形。所以整幅图的笔画数应为：1+1=2。故图5为两笔画图形。

 

　　了解了一笔画&多笔画考点的方法和注意事项之后，我们可以看看这一考点在具体题目中的呈现：

 

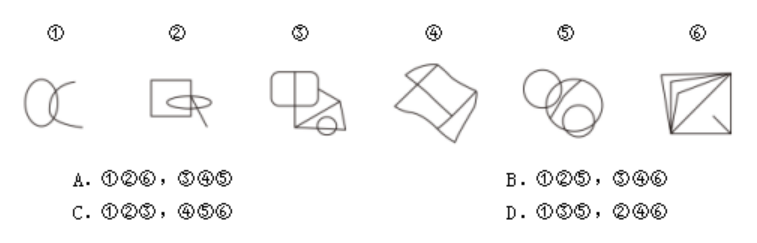
　　【例】把下面的六个图形分为两类，使每一类图形都有各自的共同特征或规律，分类正确的一项是( )

 

　　

 

　　【解析】B。①②⑤均为一笔画图形，③④⑥均为两笔画图形。