公务员考试行测中数量关系部分，工程、行程等一类M=A×B型问题频频出现，而大家最常使用的解题方法就是方程法。虽然方程法确实能够帮助我们解决很多问题，但对有些题目来说列方程并不是最优的途径，甚至可能会出现浪费很多时间列的方程而解不出来的情况。那么，今天就给大家简单介绍一下正反比思想解决M=A×B型问题。
一、什么是M=A×B型问题
这类问题主要涉及的是三个量之间的关系，形式如M=A×B。比如我们在考试中经常遇到的工程问题：工作总量=工作效率×工作时间，或是行程问题：路程=速度×时间。诸如此类的问题，我们都可以归为M=A×B型问题。
二、正反比思想
正反比思想基于的是比例关系，而其应用环境是题目中存在M=A×B的关系且存在不变量。比如在工程问题中，如果工作总量一定，则工作效率和工作时间成反比关系、如果工作时间一定，则工作效率和工作总量成正比关系，这其实就是正反比思想的应用。即两个量的乘积为一个定值时，这两个量成反比关系。两个量的商为一个定值，这两个量成正比关系。
三、方法对比
例1：经技术改进，A、B两城间列车的运行速度由150千米/小时提升到250千米/小时，行车时间因此缩短了48分钟，则A、B两城间的距离为：
A.300千米 B.291千米 C.319千米 D.320千米
【解析】
方法一：方程法
设A、B两城间的距离为S千米，则根据两次时间差为48分钟列出等量方程为：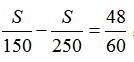
，最后解得S=300千米，选择A。
方法二：正反比思想
因为路程一定，而提速前后两次速度比为3:5，则两次时间比为5:3，时间差的2份对应时间实际量的差值48分钟，则一份对应24分钟。那么，按照150千米/小时速度行驶全程的时间为5份，对应120分钟即2小时。则A、B两城间的距离为150千米/小时×2小时=300千米，选择A。
【对比】做到这，有人会觉得这两种方法的速度差不多，但对于方程法来说，通分还是比较麻烦的。如果从这我们还是看不出来正反比明显优势的话，那么不妨再看一道题。
例2：某部队从驻地乘车赶往训练基地，如果将车速提高1/9，就可比预定的时间提前20分钟赶到;如果将车速提高1/3，可比预定的时间提前多少分钟赶到?
A.30 B.40 C.50 D.60
解析：C。对于这道行程问题来说并未给出路程、速度相关的实际量，只是给出了一些比例关系。那么这个时候，再去列方程就会很复杂，你需要设两个未知量再去求解。而如果使用正反比思想去解决就会简单很多。
提速前后的速度比为9:10，因为路程一定，则时间成反比为10:9。时间差了20分钟对应一份，那么提速前走完全程的时间为10份，即200分钟。而第二个过程的速度比为3:4，因路程一定，则两次时间之比为4:3。而200分钟对应的是4份，那么一份为50分钟。而两次时间的差值也为一份，即50分钟，则这道题选择C。
相信对比上面这两道题，大家会有明显的体会就是：方程法虽是常用的方法，但有时并不是最优选择。而正反比思想解题更为灵活，具有普适性。大家在日后做题的时候，不应只是死守“旧工具”，而应该接受新方法，并熟练的应用，这样才能在考试中游刃有余，力争上游!
