近几年来,在行测数量关系的考查中,有一种几何问题出现的频率稳步上升,其题干特点主要体现在:出现“东、南、西、北”并结合角度的方位描述,因需结合方位角度画图,让人无从下手,但是只要按照题中方向和角度画出图形,按照既定步骤便可求解。
步骤一:结合方位画出几何图形;
步骤二:结合图形中的方位角确定或构建直角三角形;
步骤三:把所求线段放在直角三角形中,并解直角三角形。
例题、一艘军舰以每小时20km的速度向东行驶,行驶A时看到一个灯塔C在北偏东60°处,军舰继续以原速向正东方向行驶,3小时后,到达B处,瞭望灯塔C,发现灯塔C在北偏东15°处,则此时军舰与灯塔的高距离为( )km。
A.30
B.30√2
C.30√3
D.45√2
【答案】B。
解析:步骤一:结合题干描述方位画图如下:
军舰最终行驶至B点,∠EAC=60°,∠CBF=15°,此题所求为军舰行至B处时与灯塔C的距离,即为BC。
步骤二:确定直角三角形,本题中无直角三角形,需构建直角三角形,作BG⊥AC,则△AGB、△BGC均为直角三角形。
步骤三:解直角三角形。
在Rt△AGB中,∠GAB=90°-∠EAC=30°,AB=20×3=60km,BG=AB÷2=30km,在△ABC中,∠C=180°-∠CAB-∠ABC=180°-30°-(90°+15°)=45°,则在Rt△BGC中,BC=√2BG=30√2,故本题选择B项。
几何方向角问题,牢记三步骤:一画,二直,三解;谨记顺口溜:方位画图是关键,构造直角当为先,特殊角度当用巧,线条长度马上现。


 更多行测技巧与方法扫码获取
更多行测技巧与方法扫码获取
 行测数量关系技巧方法案例
行测数量关系技巧方法案例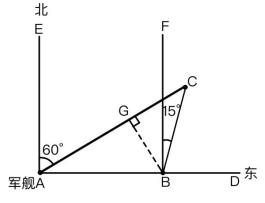
 行测备考提醒
行测备考提醒 行测技巧还没掌握?扫码回复“咨询老师”
行测技巧还没掌握?扫码回复“咨询老师”

