枚举归纳在数学中是一种非常重要的思想,在数量关系中也一种比较基础的方法。枚举是将所有需要情况逐个列举。这种方法有时看上去繁琐,但是是找不到思路时的最直观思维。归纳在数量关系中,往往可以从最初开始枚举出第一步、第二步、第三步,然后探索、猜测规律,再通过下一步验证,如果未遇反例,就基本可以确定规律。枚举归纳法适合题型:日期推断、规律探索、几何计数/构造等。
【例1】小王在商店消费了90元,口袋里只有1张50元、4张20元、8张10元的钞票,他共有几种付款方式,可以使店家不用找零钱?
A.5B.6
C.7D.8
【答案】C
【解析】
第一步,本题考查经济利润问题,用枚举法解题。
第二步,枚举如下:
可得,共有7种付款方式,可以使店家不用找零。
因此,选择C选项。
【例2】一条直线将一个平面分成2个部分,两条直线最多将一个平面分成4个部分,……
则6条直线最多将一个平面分成的部分为:
A.20B.21
C.22D.23
【答案】C
【解析】
第一步,本题考查平面几何问题中的几何计数,用枚举归纳法求解。
第二步,第1条直线最多将平面分成2块,第2条直线最多将平面分成4块,枚举发现第3条直线最多将平面分成7块,枚举发现第4条直线最多将平面分成11块。平面数依次为:2,4,7,11……,相邻两项做差得2,3,4……是公差为1的等差数列。那么以此类推,第5条直线最多将平面分成11+5=16(块),第6条直线最多将平面分成16+6=22(块)。
因此,选择C选项。


 更多行测技巧与方法扫码获取
更多行测技巧与方法扫码获取
 行测数量关系技巧方法案例
行测数量关系技巧方法案例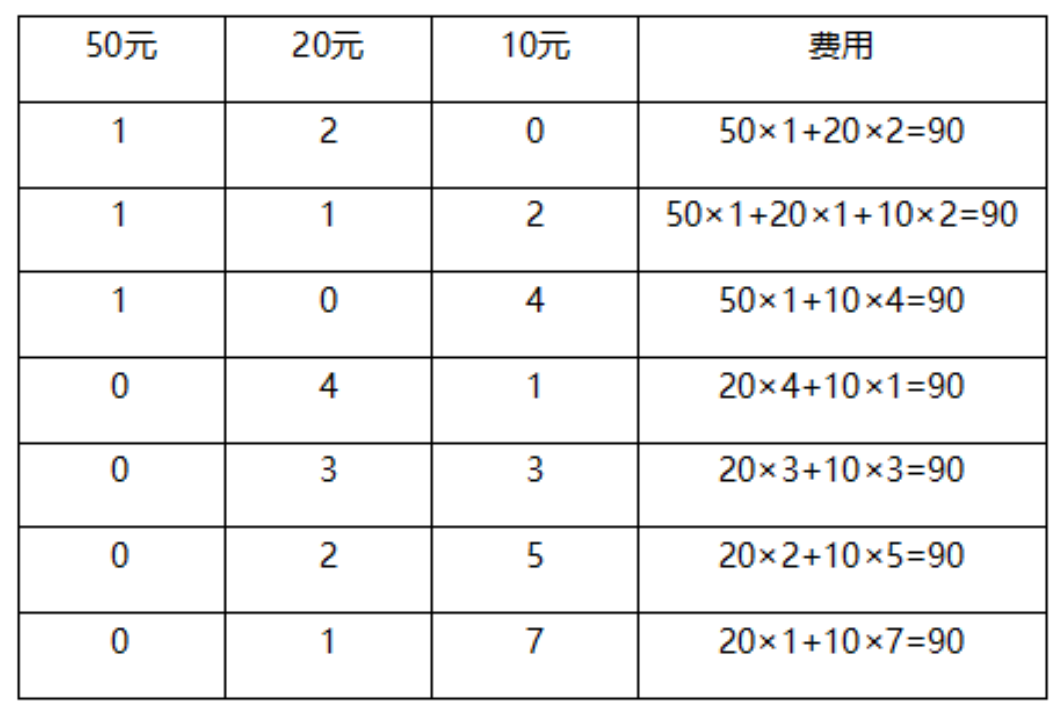
 行测备考提醒
行测备考提醒 行测技巧还没掌握?扫码回复“咨询老师”
行测技巧还没掌握?扫码回复“咨询老师”

